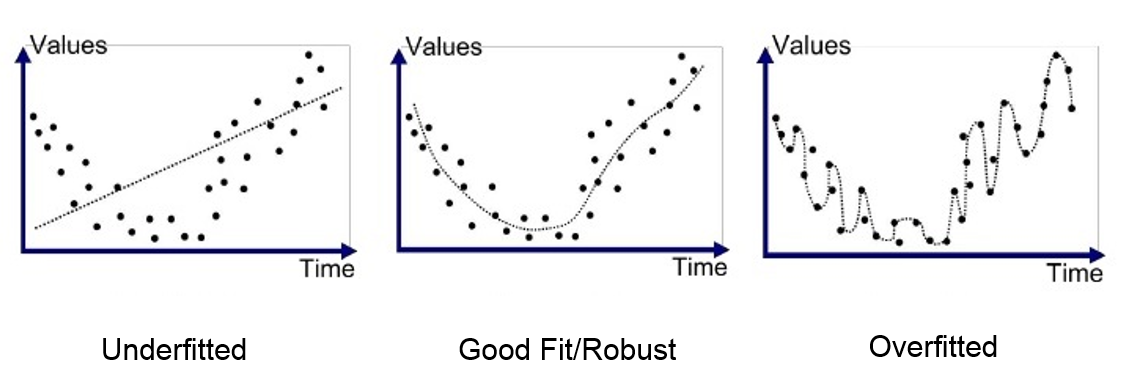
Hình ngoài cùng bên phải thể hiện một mô hình phức tạp nhưng sẽ không đạt được độ chính xác với các mẫu dữ liệu mới. Lấy một ví dụ với bài toán hồi quy logistic. Ở đây ta có mô hình của dữ liệu như sau:
Tương ứng với mô hình này, hàm cost của mô hình là:
Ta thấy, đây là một mô hình phức tạp với số mũ cao nhất là 5. Mô hình sẽ trở nên đơn giản khi ta loại bỏ các thành phần bậc cao (tương ứng với việc các giá trị
bằng 0.Mặt khác, ta có thể thấy thành phần regularization mới thêm vào là tổng bình phương của các giá trị
do đó nếu là khác 0, tức là thành phần regularization sẽ càng lớn, đồng nghĩa với việc mô hình sẽ không còn chính xác một cách hoàn toàn do giá trị hàm cost tăng lên (ta gọi đây là penalty với mỗi giá trị ).Ở trên là phần trình bày về mặt toán học, vậy câu hỏi đặt ra là, liệu ta có chắc việc tăng giá trị hàm cost (giảm overfitting) sẽ giúp mô hình đạt được độ chính xác cao hơn với tập dữ liệu mới?
