Lập trình động là một phương pháp giải các bài toán phức tạp bằng cách chia bài toán lớn thành các bài toán nhỏ hơn cùng với việc lưu lại giá trị của các bài toán nhỏ hơn này để tránh việc phải thực hiện lại các thao tác này. Những bài toán có thể áp dụng lập trình động có những thuộc tính sau:
1. Overlapping Subproblems (ví dụ dãy fibonacci khi tính toán fib(5) và fib(6) ta đều phải tính toán fib(4)).
2. Optimal Substructure
1) Overlapping Subproblems
Giống như thuật toán Chia để trị (Divide and Conquer), lập trình động bao gồm các kết quả của subproblems. Trong lập trình động, kết quả của các bài toán con sẽ được lưu vào 1 bảng để ta có thể truy cập trực tiếp thay vì tính toán lại các bài toán con này. Do đó, DP sẽ không hữu dụng khi mà các subproblems không có sự trùng lặp (overlapping) khi tính toán. Vi dụ như Binary Search sẽ không có các subproblems chung; ngược lại đối với bài toán Fibonacci, sẽ có rất nhiều subproblems được tính toán lại nhiều lần.
/* simple recursive program for Fibonacci numbers */
int fib(int n)
{
if ( n <= 1 )
return n;
return fib(n-1) + fib(n-2);
}
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
Ta thấy rằng fib(3) được gọi 2 lần, do đó, nếu ta lưu giá trị fib(3) thì thay vì phải tính toán lại, ta chỉ cần truy cập trực tiếp kết quả này. Ta có hai phương pháp để lưu các giá trị giống như fib(3) là Memoization(Top down) và Tabulation(Bottom up).
a) Memoization(Top down)
Phương pháp này giống với recursion nhưng trước khi ta tính toán 1 subproblems, ta sẽ tìm trong một bảng. Nếu subproblems này chưa được tính toán, ta sẽ tính toán và lưu vào trong bảng, ngược lại, ta sẽ trả lại trực tiếp giá trị của bảng.
def fib(n, lookup):
if n == 0 or n == 1 :
lookup[n] = n
if lookup[n] is None:
lookup[n] = fib(n-1 , lookup) + fib(n-2 , lookup)
return lookup[n]
b) Tabulation(Bottom up)
Phương pháp này ta xây dựng một bảng từ subproblems nhỏ nhất đến lớn nhất và cuối cùng trả về giá trị cuối cùng trong bảng. Ví dụ, cùng với bài toán Fibonacci, ta đầu tiên tính toán fib(0), sau đó fib(1), fib(2), fib(3) v.v...
def fib(n):
f = [0]*(n+1)
f[1] = 1
for i in xrange(2 , n+1):
f[i] = f[i-1] + f[i-2]
return f[n]
|
Both Tabulated and Memoized store the solutions of subproblems. In Memoized version, table is filled on demand while in Tabulated version, starting from the first entry, all entries are filled one by one. Unlike the Tabulated version, all entries of the lookup table are not necessarily filled in Memoized version. For example, Memoized solution of the LCS problem doesn’t necessarily fill all entries.
2) Optimal Substructure
Một bài toán có tính chất optimal substructure nếu optimal solution của bài toán lớn có thể tìm ra thông qua optimal solution của các bài toán con.
Ví dụ trong thuật toán tìm đường đi ngắn nhất Shortest Path, ta nếu ta có node
X nằm trên cung ngắn nhất từ một node nguồn
u đến một node đích
v thì đường đi ngắn nhất từ u tới v sẽ là combination của đường đi ngắn nhất từ
u tới
X và từ
X tới
v.
Ngược lại bài toán Longest Path không có tính chất này. Ví dụ với đồ thị dưới đây:
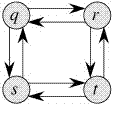
Ta sẽ có hai đường dài nhất từ q tới t (không kể các cung có cycle) là: q→r→t và q→s→t . Ở đây, ví dụ longest path q→r→t sẽ không là combination của longest path từ q→r và r→t bởi vì longest path từ q tới r và từ r tới t lần lượt là q→s→t→r và r→q→s→t.















