Logistic Regression được sử dụng trong bài toán Binary Classification nghĩa là output chỉ nhận hai giá trị là 0 và 1. Ví dụ đầu và là 1 bức ảnh:
Khi này, đầu ra của ta sẽ là 0 hoặc 1 tương ứng với không có mèo trong ảnh và có mèo trong ảnh.
Nhưng giá trị Ŷ được tính như sau:
Ta có thể thấy, giá trị này có thể là một số thực tùy ý, khi đó, ta sẽ phải áp dụng một hàm biến đổi để biến giá trị thực này thành các giá trị 0 hoặc 1.
Từ đây ta có khái niệm mới là activation function nghĩa là hàm dùng để biến đổi đầu ra thành các giá trị ta mong muốn, ví dụ trong bài toán này ta chỉ quan tâm đến giá trị 0 hoặc 1, sigmoid function có thể được chọn là activation function và được định nghĩa như sau
Ở đây z cũng chính là giá trị Ŷ (số thực ta nhận được). Để thấy rõ hơn ta có thể nhìn đồ thị của hàm sigmoid.
Giá trị sau hàm sigmoid làm 1 số nằm trong khoảng 0 và 1 và thường xấp xỉ 2 giá trị này nên ta có thể dùng signmoid function. Vấn đề là, ta biết có 1 xác xuất rất nhỏ nhưng giá trị sigmoid có thể không gần giá trị 0 hoặc giá trị 1, ví dụ khi z = 0, signmoid = 0.5, khi này ta sẽ xử lý như thế nào? Có phải ta chấp nhận một lượng rất nhỏ sai số khi sử dụng hàm sigmoid?
Tiếp theo ta sẽ nhìn vào cost function của Logistic Regression, ta nên phân biệt giữa cost function và loss function.
Loss function tính toán lỗi cho chỉ 1 training sample
Trong khi Cost function là trung bình cộng của tất cả các loss function trong toàn bộ tập training. Bình thường, nếu giá trị trong grouth truth là y và giá trị ta thu được sau sigmoid function là Ŷ, ta có thể nghĩ ngay tới việc tính loss function như sau:
Việc ta bình phương là để tránh trường hợp giá trị này là âm cũng tương tự như ta lấy giá trị tuyệt đối, loss luôn phải dương và giá trị 1/2? Oh tại sao ta lại chọn là 1/2 nhỉ? Câu trả lời ở đây:
https://datascience.stackexchange.com/questions/10188/why-do-cost-functions-use-the-square-error
Nhưng trong thực tế, loss function sẽ được định nghĩa khác.
Ta thấy rõ ràng nếu theo (1) thì công thức sẽ dễ dàng hơn nhiều.
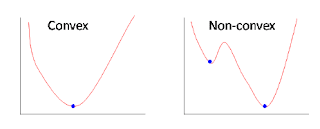
Nhưng vấn đề ở đây ta đang muốn tối ưu hàm L này, và trong bài toán tối ưu, nếu hàm loss là (1), khi đó sẽ có dạng như bên phải hình dưới đây, và là 1 dạng hàm non-convex (hàm không lồi), bởi vì nó sẽ có rất nhiều điểm cực tiểu. Ở trong hình bên phải, điểm cực tiểu là 2 điểm xanh với điểm cao hơn là cực tiêu địa phương (local optima) và điểm thấp là cực tiểu toàn cục (global optima) - là điểm mà ta muốn tìm ứng với giá trị hàm loss là nhỏ nhất.
Với hàm số (2), lúc này dạng đồ thị sẽ là convex, khi đó chỉ có 1 cực tiểu duy nhất, lúc này việc tối ưu để tìm thông số ứng với điểm cực tiểu của hình bên trái sẽ đơn giản hơn nhiều, để tìm cực tiểu này, ta áp dụng thuật toán Gradient Descent được trình bày ở bài sau.
Với logistic regression, tổng quát lại, ta cần thay đổi các tham số w và b như hình dưới đây để có được giá trị hàm loss là nhỏ nhất.





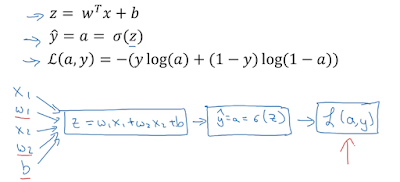
Không có nhận xét nào:
Đăng nhận xét