Lý thuyết thông tin tính toán lượng thông tin có mặt trong một tập sự kiện. Lượng thông tin này bị ảnh hưởng trực tiếp từ tính khả đoán được của sự kiện (Predictability).
Vậy Predictability là gì?
- Sự kiện mà ta đoán trước được kết quả sẽ không mang thông tin (zero information)
- Sự kiện có ít biến cố mang ít thông tin: ví dụ như tung đồng xu chọn mặt úp hay ngửa
- Những sự kiện ngẫu nhiên mang nhiều thông tin
In information theory, chaos processes more information
Thông tin của 1 sự kiện được định nghĩa bằng công thức.
I(x)=−log(P(x))
Trong lý thuyết thông tin, entropy là đại lượng được dùng để tính toán lượng thông tin của 1 sự kiện.
Ta định nghĩa entropy là:
H(x)=Ex∼P[I(x)]
Thay I(x) ở trên vào ta được entropy của 1 sự kiện được tính như sau:
H(x)H(x)=−Ex∼P[logP(x)]=−∑xP(x)logP(x)
Nếu log có base là 2 thì H(x) đang tính toán số bit cần thiết để mã hóa 1 thông tin. Trong information theory, lượng thông tin và độ ngẫu nhiên của sự kiện tương quan với nhau (positively correlated). Giá trị entropy cao tương đương với độ ngẫu nhiên cao và ta cần nhiều bit để mã hóa.
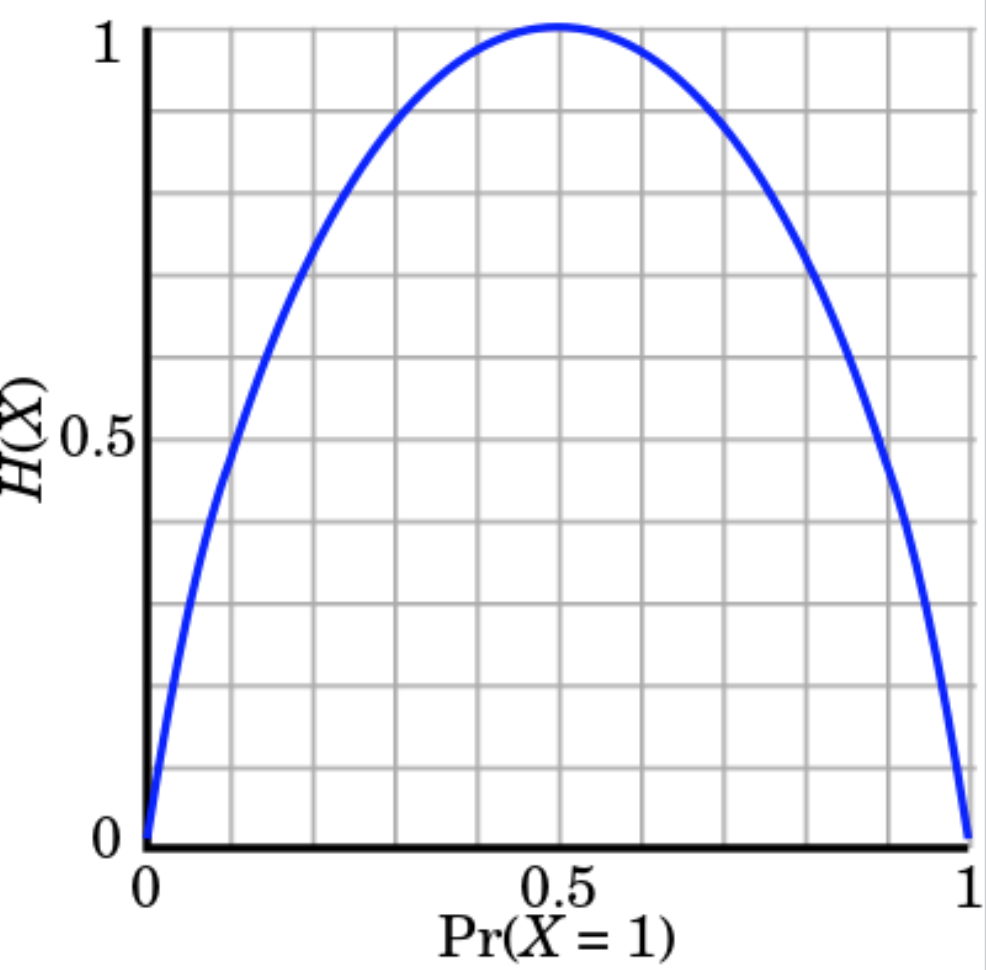
Để tính toán entropy của việc tung đồng xu (với điều kiện đồng xu là tiêu chuẩn).
H(X)=−p(head)⋅log2(p(head))−p(tail)⋅log2(p(tail))=−log212=1
Do đó ta sẽ chỉ cần 1 bit để thể hiện tập biến cố của phép thử này 0/1.
Ngoài ra, lượng thông tin là lớn nhất khi và chỉ khi p(head) = p(tail) = 0.5
Với 1 con xúc sắc lập phương, entropy là H(X)=
log26≈2.59
Con xúc sắc có entropy cao hơn đồng xu bởi biến độ khó đoán định hơn (less predictable)
Nếu entropy tính toán lượng bit nhỏ nhất để mã hóa thông tin cho trước, cross entropy được sử dụng để tính toán số bit tối ưu để mã hóa phân phối P khi ta sử dụng phân phối Q.
Dễ hiểu hơn, ta có thể coi P là ground truth và Q là prediction. Do vậy hàm loss của ta cũng chính là số bit tối ưu để có thể match hai phôn phối này lại với nhau.
H(P,Q)=−∑xP(x)logQ(x)
In deep learning, P is distribution of the true labels, and Q is the prob. distribution of predictions from the deep network.
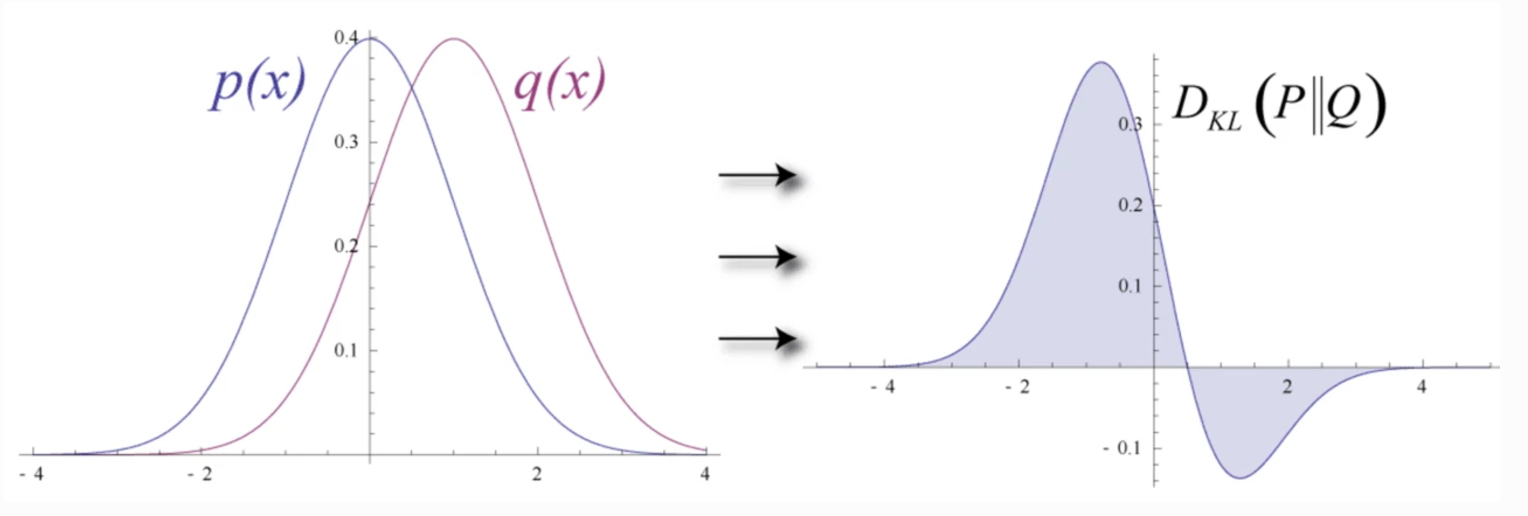
Trong Deep Learning, ta muốn xây dựng một model để mô hình phân phối Q từ phân phối P của data đã cho trước (training data). Sự khác nhau giữa hai phân phối P và Q có thể được tính toán bằng KL Divergence như sau.
DKL(P||Q)=ExlogP(x)Q(x)
Ta được:
DKL(P||Q)=∑x=1NP(x)logP(x)Q(x)=∑x=1NP(x)[logP(x)−logQ(x)]
Tuy nhiên ta có thể thấy KL Divergence là không đối xứng. D(P||Q) != D(Q||P)
Và ta có:
H(P)H(P,Q)DKL(P||Q)=−∑PlogP, - entropy=−∑PlogQ, - cross entropy và=∑PlogPQ. - KL divergence
Do đó ta có thể viết lại cross-entropy như sau:
H(P,Q)H(P,Q)=−∑PlogQ=−∑PlogP+∑PlogP−∑PlogQ=H(P)+∑PlogPQ=H(P)+DKL(P||Q)
Hay cross entropy = KL + entropy
Cross entropy H(P,Q) lớn hơn entropy H(P) do ta cần nhiều bit hơn để có thể mã hóa dữ liệu với Q (P khác Q). Do đó, ta có thể chứng minh rằng, KL-div luôn dương khi P khác Q và bằng 0 khi P = Q.
Từ đây, ta thấy rằng KL-div có thể dùng để tính sự sai khác (discrepancy) giữa 2 distribution.
Ta lại có H(P) chỉ phụ thuộc vào phân phối ta đang có, ví dụ tung đồng xu thì H(P) = 1. H(P) không bị ảnh hưởng bởi model ta xây dựng, do vậy, tối ưu giá trị cross entropy tương đương với việc tối ưu KL-div.
lo
H(P,Qθ)∇θH(P,Qθ)=H(P)+DKL(P||Qθ)=∇θ(H(P)+DKL(P||Qθ))=∇θDKL(P||Qθ)
- Maximum Likelihood Estimation
Ta muốn xây dựng một mô hình để cực đại hóa giá trị xác suất của 1 biến cho trước - Maximum Likelihood Estimation or MLE (ví dụ trong training set ta có điểm dữ liệu x, do đó xác suất xuất hiện thưc tế của điểm này là 1) - hoặc nói cách khác mô hình của ta khớp với dữ liệu nhất có thể.
θ^=argmaxθ∏i=1Np(xi|θ)
Nhưng việc nhân các giá trị như trên có thể dễ dàng dẫn đến việc tràn số (overflow) hoặc underflow. Do đó ta chuyển công thức trên về dạng log để tránh vấn đề này.
Tuy nhiên, các optimizer thông thường sẽ chỉ hỗ trợ việc minimize một hàm loss cho trước. Do vậy thay vì tối ưu trực tiếp trên MLE, ta áp dụng log và tối ưu giá trị nghịch đảo hay còn được gọi là negative log likelihood (NLL).
θ^=argminθ−∑i=1Nlogp(xi|θ)
Khi này NLL và việc tối ưu cross entropy trở nên tương đương do:
θ^=argminθ−∑i=1Nlogq(xi|θ)=argminθ−∑x∈Xp(x)logq(x|θ)=argminθH(p,q)
Trong công thức trên ta thêm p(x) do p(x) đại diện cho data đã cho trước, có thể coi như là 1 đại lượng không đổi, do vậy việc tối ưu là tương đương khi thêm 1 hẳng số.
Ta xây dựng 1 mô hình để khớp với dữ liệu cho trước nhất có thể. Ta bắt đầu với MLE sau đó chuyển sang NLL để tránh việc over/underflow. Về mặt toán học thì NLL và cross entropy là tương đương. KL-div là một hướng tiếp cận khác nhưng nhìn chung với các công thức khác nhau, ta vẫn sẽ tìm được một optimal point giống nhau.
Trong các bài toán hồi quy, ta có y= f(W,x). Và trong các vấn đề thực tế, ta thường gặp phải uncertainty và việc thông tin bị khuyết. Do đó, ta có thể mô hình bài toán thao phân bố Gaussian:
y^=f(x;θ)y∼N(y;μ=y^,σ2)p(y|x;θ)=1σ2π−−√exp(−(y−y^)22σ2)
Lúc này log likelihood trở thành việc optimize MSE.
J∇θJ=∑i=1mlogp(y|x;θ)=∑i=1mlog1σ2π−−√exp(−(y(i)−y(i)^)22σ2)=∑i=1m−log(σ2π−−√)−logexp((y(i)−y(i)^)22σ2)=∑i=1m−log(σ)−12log(2π)−(y(i)−y(i)^)22σ2=−mlog(σ)−m2log(2π)−∑i=1m(y(i)−y(i)^)22σ2=−mlog(σ)−m2log(2π)−∑i=1m∥y(i)−y(i)^∥22σ2=−∇θ∑i=1m∥y(i)−y(i)^∥22σ2
Many cost functions in deep learning including the MSE, can be dervied from the MLE